The spontaneous electric polarization in response to an externally applied electric field is what is referred to as ferroelectricity. The electric polarization, $P$, in most cases is proportional to the applied electric field. For review the polarization is give by:
\begin{align}
\mathbf{P} &= N\mathbf{\mu}_{D} = \alpha \mathbf{E} \\
\alpha &= \alpha_{e^{-}}+\alpha_{ion}+\alpha_{mol}
\end{align}
where $N$ is the dipole number density. The polarizability coefficient is contribution from electric, ionic, and molecular dipoles.
When the response is linear the material is classified as being dielectric, elsewise its referred to as being paraelectric. The paraelectric behavior is strongly tied to temperature and disappears at the Curie temperature ($T_c$). When a spontaneous remanent electric polarization occurs upon removal of an applied electric field the material is termed ferroelectric; these materials show typical hysteresis behavior.
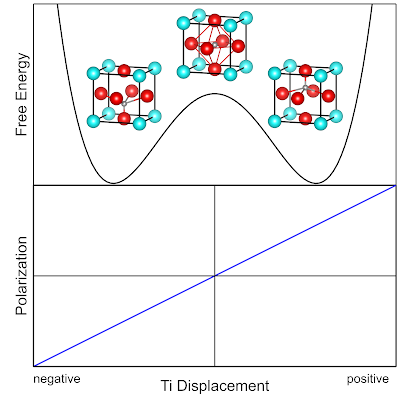
One of the most ubiquitous materials that shows ferroelectric behavior is Barium Titanate ($\text{BaTiO}_3$). The $\text{BaTiO}_3$ crystal has a Tetragonal unit cell, i.e. all angles are 90 degrees but only two sides have the same length ($a=b\neq c$). The species tend to be predominately in an ionic electronic structure configuration, i.e., species at the lattice sites behave like anions and cations. The $\text{Ti}^{+4}$ cation in $\text{BaTiO}_3$ sits in the center of the unit cell and can occupy several slightly off center positions that give rise to a static permanent electric dipole moment. In the illustration below the free energy profile, unit cell with Ti displacement (grey atom) and the change in electric polarization is qualitatively shown.
Curie temperature each unit cell has a randomly oriented electric dipole moment and thus no bulk permanent moment. Below the Curie temperature the exchange interactions between the individual electric dipole moments will cause some preferred orientation. The Curie temperature for several ferroelectric materials is listed in the table below:
| Material | Curie Temperature [K] |
|---|---|
| α-Fe | 1043 |
| PbTiO3 | 763 |
| PbZrO3 | 506 |
| BaTiO3 | 400 |
| NaNbO3 | 336 |
| ZnTiO3 | 278 |
| NH4H2PO4 | 148 |
The change in free energy as a function of spontaneous polarization and temperature follows a double well potential typically given by the Ginzburg-Landau theory. The result is a free energy expression written in terms of expansion coefficients that capture the materials spontaneous polarization while accounting for crystal/anisotropy effects. An example of temperature dependence is given below highlighting that at elevated temperatures the spontaneous polarization is weak and therefore polarization is dominated by a paraelectric response.
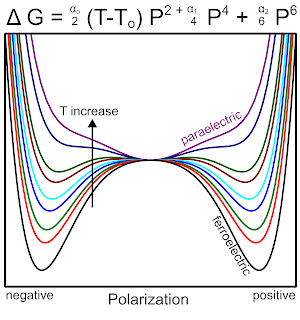 |
| Free energy as a function of polarization and temperature, illustrative example showing how a material transitions from ferroelectric to paraelectric. |
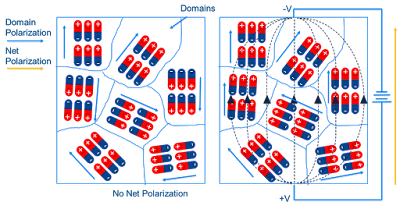 |
| Example of domain polarization and external field induced net polarization (image adapted from https://ec.kemet.com/dielectric-polarization) |
In the presence of an applied external electric field, the individual domains can will be driven to align with the field direction as to minimize the free energy, $ G = P_{i}E_{i}$. One can also write the difference in free energy, $\Delta G$, due to changes in the domain orientation such that:
\begin{align}
\Delta G &= G_{P_1} - G_{P_2} \\
&= \Delta P^s E_{i} + \frac{1}{2} \Delta \chi_{ij} E_i E_j
\end{align}
in the expressions above we use $i,j,\cdots$ tensor notation (a.k.a Einstein summation) to indicate coordinates. The term $P^s$ is the spontaneous polarization term and $\chi_{ij}$ susceptibility tensor. The $\Delta$ in front of the material parameters indicates the difference in values between the two states. The change in free energy drives the domains so that they both align and spatial grow until a saturation condition is meet. The change in domain structure has lowered the configurational entropy and "poled" domain structure no longer remembers the initially random polarization configuration. This leads to a a hysteresis curve, where upon reversal of the applied electric field a different polarization configuration is sampled. I will have a blog on hysteresis phenomena.
The quote for today is an excerpt from one of the original documents highlighting the discovery of electric polarization and piezoelectric effects in a mineral salt (Rochelle salt):
"It appears then, that the asymmetry of the throws in Anderson's experiment is due to a hysteresis in electric polarization analogous to magnetic hysteresis. This would suggest a parallelism between the behavior of Rochelle salt as a dielectric and steel, for example, as a ferromagnetic substance."
- Joseph Valasek, APS Minutes, 1920
References & Additional Reading
Reuse and Attribution